• Помощь в изучению функции
• Линейная функция. Авторы: "Гекель, Гапошкина"Квадратичная функция. Авторы:"Хомутова Ангелина"Показательная и логарифмическая функцииПостроение графиков функций в ExcelГипербола в математике

 

Показательная функция.  
Показательная функция — математическая функция , где a называется «основанием», а x — «показателем» степени.

Основные свойства показательной функции y = a x при a > 1:

• Область определения функции - вся числовая прямая.
• Область значений функции - промежуток (0;+).
• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1 < ax2 .
• При x = 0 значение функции равно 1.
• Если x > 0 , то a x > 1 и если x < 0, то 0 < a < 1.

Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.

Основные свойства показательной функции y = a x при 0 < a < 1:

• Область определения функции - вся числовая прямая.
• Область значений функции - промежуток (0;+).
• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1 > ax2 .
• При x = 0 значение функции равно 1.
• Если x > 0 , то 0 < a < 1 и если x < 0, то a x > 1.

К общим свойствам показательной функции как при 0 < a < 1, так и при a> 1 относятся:

• ax1 ax2 = ax1+ x2, для всех x1 и x2.
• a−x=(ax)−1=1ax для любого x.
• nax=axn  для любого x и любого nNn=1 .
• (ab)x = ax bx для любых a, b > 0; a,b=1 .
• (ba)x=bxax  для любых a, b > 0; a,b=1 .
• ax1 = ax2, то x1 = x2.

Логарифмическая функция.
Логарифмическая функция у = loga x (а > 0, a # 1 ) определена только при х > 0 (у = loga x <=> х = аy) и обладает следующими свойствами:
1. монотонности: 0 < x1 < x2<=>

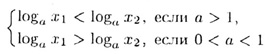
2. сохранения знака:у = loga x > 0 <=>

3. асимптотического стремления к бесконечности: при х —> 0 (x > 0),
Прямая х = 0 называется вертикальной асимптотой графика функции у = loga x.

«Практическое применение логарифмической и показательной функций».
География
«Без знания математики нельзя понять ни основ современной техники, ни того, как учёные изучают природные и социальные явления».
Колмогоров А.Н.
Для планирования развития городов, других населённых пунктов, строительства жилья, дорог, других объектов мест проживания людей, необходимы расчёты – прогнозы на 5, 10, 20 лет вперёд.
Покажем, как в таких расчётах применяются показательная функция и логарифмы.
Задача №1. Население города возрастает ежегодно на 3%. Через сколько лет население этого города увеличиться в 1,5 раза?
Решение. Для решения этой задачи применим формулу сложных процентов:
 Примем население города за a, тогда А = 1,5а, p = 3 и x – неизвестно. Сделав подстановку в формулу и сократив на а, получим:
 или
Чтобы решить это показательное уравнение прологарифмируем его.
xlg1,03 = lg1,5 , откуда x =
Найдя по таблице lg1,5 и lg1,03 , получим

                Ответ: Примерно через 14 лет.

 

 

Расчёты в производстве
«Прежде всего, возьмём математику. Общий отдел её, имеющий дело с цифрами, оказывает помощь во всякой промышленной деятельности».
Спенсер Г. 
Приведём примеры, демонстрирующие применение показательной функции в экономических расчётах производства. Наукой и практикой экспериментально установлены многие зависимости между величинами, поэтому некоторые формулы, которые будут нами использоваться, мы приводим без вывода.  
               Так, стоимость оборудования цеха через t лет может быть найдена по формуле , где  – первоначальная стоимость оборудования в рублях, p – ежегодный процент амортизации, В – стоимость оборудования в рублях через t лет. Необходимо вычислить стоимость оборудования через 5 лет, если его первоначальная стоимость , а ежегодный процент амортизации  = 5,7%
Решение. Подставим заданные величины в формулу. Получим:

Задача: Стоимость оборудования мастерской равна 500 тыс. р. Известно, что через 10 лет стоимость этого оборудования вследствие амортизации будет равна 200 тыс. р. Найдите процент ежегодной амортизации оборудования.
Решение.  где B = 200 тыс. рублей, тыс. рублей, x = 10 лет.
 
 
(%)
Ответ: ежегодный процент амортизации составляет 8,76 %.
Биология
«В нашу современную жизнь вторгается математика с её особым стилем мышления, становящимся сейчас обязательным и для инженера, и для биолога».
Гнеденко Б.В.
Задача №1. В начальный момент времени было 8 бактерий, через 2 ч после помещения бактерий в питательную среду их число возросло до 100. Через сколько времени с момента помещения в питательную среду следует ожидать колонию в 500 бактерий?
Решение. В обозначениях задачи «0» эти данные записываются следующим образом:   
Значит, требуемое время соответствует значению выражения , т.е. примерно через 3 ч 15 мин.
Задача №2. Численность популяции составляет 5 тыс. особей. За последнее время в силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида?
Решение.  Применим для вычисления времени формулу сложных процентов:  где
2 тыс. – численность животных по истечению искомого времени;
5 тыс. – численность животных в начальный момент времени;
p = 8 - % сокращения численности животных.
Предварительно разделив обе части уравнения на 1000, получим:

  
 лет.
Ответ: приблизительно через 11 лет.
Физика
«Математические методы становятся не только методами, которые используются в механике, физике, но общими методами для всей науки в целом»
Соболев С.Л.
                Например. Для урана-238 Т = 4,56 млрд. лет; для радия-226 Т = 1590 лет; для цезия-137 Т = 31 год; для йода-131 Т = 8 суток; для радона-222 Т = 3,81 суток.
Пусть Т – период полураспада радиоактивного вещества, а t – время, прошедшее с начала наблюдения. Отношение  – мера протекшего времени при условии, что за единицу времени берётся период полураспада. Тогда,  где – масса вещества в начальный моментt = 0, а m – масса вещества по прошествии времени t. Если взять t=T , то получим , т.е. остающаяся в результате распадамасса составляет половину исходной массы. Так и должно быть по определению  самого понятия периода полураспада.
Задача №1. Чему равна масса йода-131 к концу четвёртых суток с начала наблюдения, если в начальный момент его масса составляла 1г?
Решение.   = 1г; Т = 8 сут.; t = 4 сут.; m - ?
;  г.
Ответ: m  0,7 г.
Заключение.
Логарифмы находят самое широкое применение при обработке результатов тестирования в психологии и социологии, в составлении прогнозов погоды и даже в музыке (представляя собой ступени темперированной 12-ти звуковой гаммы частот звуковых колебаний), а также других областях науки и техники.
Главное мы достигли поставленной цели и поняли, как широко применяются знания логарифмов и показательной функции.