О п р е д е л е н и е 1. Если даны числовое множество Х и правило f, позволяющее поставить в с о о т в е т с т в и е каждому элементу х из множества Х определенное число у, то говорят, что задана функция у = f(х) с областью определения Х; пишут у = f(х), х  Х. Х.
При этом переменную х называют независимой переменной или аргументом; а переменную у – зависимой переменной.

Например, соответствия f и g, изображенные на рисунке 1.1 а и б, являются функциями, а на рисунке 1.1 в и г – нет. В случае в – не каждому элементу x  X соответствует y X соответствует y  Y . В случае г не соблюдается условие однозначности. Y . В случае г не соблюдается условие однозначности.
Для области определения функции у = f(х), х  Х, иногда удобно использовать обозначение D(f). Например: для функции у = Х, иногда удобно использовать обозначение D(f). Например: для функции у = 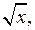 х ≥ 0 имеем D(f) = [0; + ∞); х ≥ 0 имеем D(f) = [0; + ∞);
Нельзя говорить о функции у = f(х) без указания ее области определения, которая или указывается явно, или подразумевается – в случае, если область определения функции у = f(х) совпадает с областью определения выражения f(х) (такую область определения иногда называют естественной).
Способы задания функции.
Существует несколько способов задания функции.
Табличный. Используется тогда, когда область определения состоит из конечного множества чисел. Тогда для задания функции проще всего указать таблицу, содержащую значения аргумента и соответствующие значения функции. Например, таблица логарифмов. Другим примером могут быть таблицы, содержащие данные о числе жителей, населяющих земной шар в отдельные годы, расписания движения поездов и т.п.
Аналитический. При аналитическом способе задания функция может быть задана ЯВНО, когда дано выражение yчерез x, т.е. формула имеет вид y = f (x) ; НЕЯВНО, когда xи y связаны между собой уравнением вида F(x, y) = 0; ПАРАМЕТРИЧЕСКИ, когда соответствующие друг другу значения х и у выражены через третью переменную величину t, называемую параметром.
Логический. Если функция описывается правилом ее составления, например, функция Дирихле: f(x)= 1, если x – рациональное; f(x)= 0, если x – иррациональное.
Графический. Состоит в изображении графика функции
График функции
Графиком функции (в декартовой прямоугольной системе координат) называют геометрическое место точек, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции. |

